primes.py
View source code here on GitHub!
Includes
- python.src.lib.primes.primes(stop: int | None = None) Iterator[int]
Iterates over the prime numbers up to an (optional) limit, with caching.
This iterator leverages the
modified_eratosthenes()iterator, but adds additional features. The biggest is astopargument, which will prevent it from yielding any numbers larger than that. The next is caching of any yielded prime numbers.It takes \(O(n)\) space as a global cache, where \(n\) is the highest number yet generated, and \(O(n \cdot \log(\log(n)))\) to generate primes up to a given limit of \(n, n < 2^{64}\). If \(n\) is larger than that, Python will shift to a different arithmetic model, which will shift us into \(O(n \cdot \log(n)^{1.585} \cdot \log(\log(n)))\) time.
- python.src.lib.primes.modified_eratosthenes() Iterator[int]
Iterates over prime numbers using the Sieve of Eratosthenes.
This function implements the Sieve of Eratosthenes. In general, it will iterate over all of the prime numbers. Below is a gif (courtesy of Wikipedia) that demonstrates the principle of the sieve.
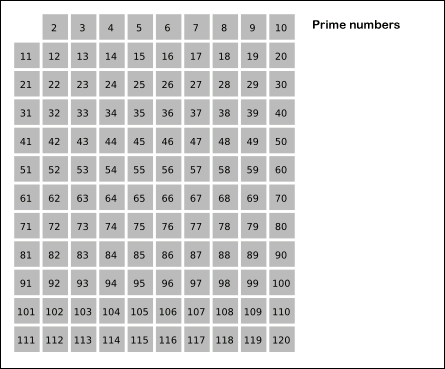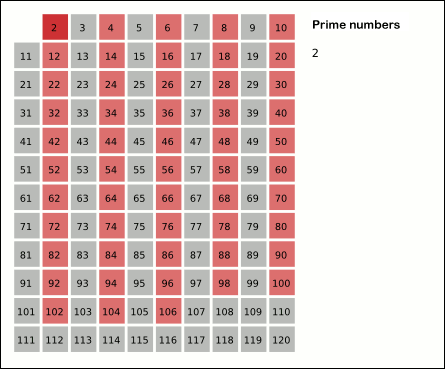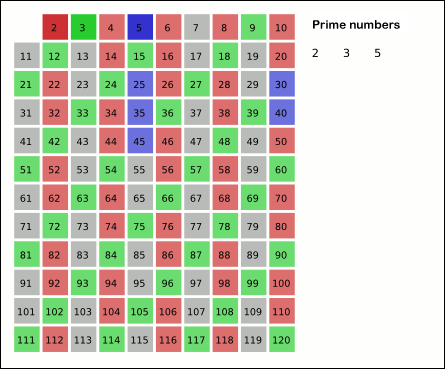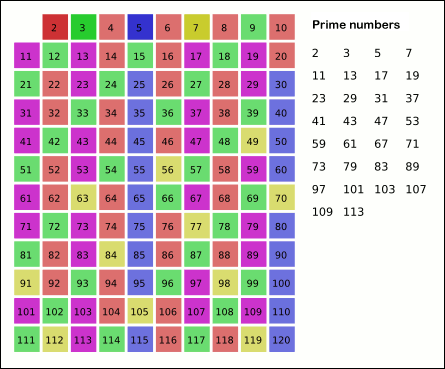
- python.src.lib.primes.prime_factors(num: int) Iterator[int]
Iterates over the prime factors of a number.
Note
For the purposes of this function, \(-1\) is included as a factor for negative numbers, and \(0\) is yielded as a special case. In general, prime factors are strictly positive integers greater than 1.
It takes \(O(m \cdot \log(m)^{1.585} \cdot \log(\log(m)))\) time to generate the needed primes, where \(m = \sqrt{n}\), so \(O(\sqrt{n} \cdot \log(\sqrt{n})^{1.585} \cdot \log(\log(\sqrt{n})))\), which simplifies to \(O(\sqrt{n} \cdot \log(n)^{1.585} \cdot \log(\log(n)))\) operations.
- python.src.lib.primes.is_prime(num: int, count: int = 1, distinct: bool = False) bool
Detects if a number is prime or not.
If a count other than 1 is given, it returns True only if the number has exactly count prime factors.
This function has three cases. If count is \(1\), this function runs in \(O(\log(n)^{1.585} \cdot \log(\log(n)))\). If count is \(c\) and
distinct=False, it runs in \(O(c \cdot \log(n)^{1.585} \cdot \log(\log(n)))\). Otherwise, it runs in \(O(\sqrt{n} \cdot \log(n)^{1.585} \cdot \log(\log(n)))\) time.
- python.src.lib.primes.primes_and_negatives(*args: int) Iterator[int]
Iterate over the primes and their negatives using
primes().
- python.src.lib.primes.fast_totient(n: int, factors: Iterable[int] | None = None) int
A faster method to calculate Euler's totient function when n has distinct prime factors.
It runs exactly 1 multiplication and 1 subtraction per prime factor, giving a worst case of \(O(\sqrt{n} \cdot \log(n)^{3.17} \cdot \log(\log(n)))\).
- python.src.lib.primes.totient(n: int) int
Calculates Euler's totient function in the general case.
This function computes the number of integers less than n that are coprime to n. It handles the general case, including repeated prime factors.
Takes \(O(\log(n))\) fraction multiplications, each of which is dominated by two GCDs, which run at \(O(\log(\min(a, b))^2)\). Given that the max factor is \(\sqrt{n}\), we can simplify this to a worst case of \(O(\log(n) \cdot \log(\sqrt{n}))^2 = O(\log(n) \cdot \tfrac{1}{2} \log(n)^2) = O(\log(n)^3)\).
Computing the prime factors themselves takes \(O(\sqrt{n} \cdot \log(n)^{1.585} \cdot \log(\log(n)))\) when the global prime cache is not initialized, but on all future runs will take \(O(\log(n))\) time.
This combines to give us \(O(\sqrt{n} \cdot \log(n)^{4.585} \cdot \log(\log(n)))\) time when the cache is stale, and \(O(\log(n)^4)\) time on future runs.
1from fractions import Fraction
2from functools import reduce
3from itertools import count, filterfalse, takewhile
4from math import ceil, sqrt
5from typing import Callable, Collection, Dict, Iterable, Iterator, Optional
6
7from sortedcontainers import SortedSet
8
9cache = SortedSet([2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61])
10last_cached: int = cache[-1]
11
12
13def primes(stop: Optional[int] = None) -> Iterator[int]:
14 """Iterates over the prime numbers up to an (optional) limit, with caching.
15
16 This iterator leverages the :py:func:`modified_eratosthenes` iterator, but adds additional features. The biggest
17 is a ``stop`` argument, which will prevent it from yielding any numbers larger than that. The next is caching of
18 any yielded prime numbers.
19
20 It takes :math:`O(n)` space as a global cache, where :math:`n` is the highest number yet generated, and
21 :math:`O(n \\cdot \\log(\\log(n)))` to generate primes up to a given limit of :math:`n, n < 2^{64}`. If :math:`n`
22 is *larger* than that, Python will shift to a different arithmetic model, which will shift us into
23 :math:`O(n \\cdot \\log(n)^{1.585} \\cdot \\log(\\log(n)))` time."""
24 if stop is None:
25 yield from cache
26 else:
27 yield from takewhile(stop.__gt__, cache)
28 global last_cached
29 if stop and last_cached > stop:
30 return
31 if stop is None:
32 secondary = modified_eratosthenes()
33 else:
34 secondary = takewhile(stop.__gt__, modified_eratosthenes())
35 for p in filterfalse(cache.__contains__, secondary):
36 cache.add(p)
37 last_cached = p
38 yield p
39
40
41def modified_eratosthenes() -> Iterator[int]:
42 """Iterates over prime numbers using the Sieve of Eratosthenes.
43
44 This function implements the `Sieve of Eratosthenes <https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes>`_. In
45 general, it will iterate over all of the prime numbers. Below is a gif (courtesy of Wikipedia) that demonstrates
46 the principle of the sieve.
47
48 .. image:: https://upload.wikimedia.org/wikipedia/commons/9/94/Animation_Sieve_of_Eratosth.gif
49 :alt: Any animated example of the Sieve of Eratosthenes"""
50 # modified_eratosthenes taken, refactored from https://stackoverflow.com/a/19391111
51 yield from (2, 3, 5, 7)
52 sieve: Dict[int, int] = {}
53 recurse = primes()
54 next(recurse)
55 prime = next(recurse)
56 if prime != 3:
57 raise ValueError() # pragma: no cover
58 prime_squared = prime * prime
59 for candidate in count(9, 2):
60 if candidate in sieve: # if c is a multiple of some base prime, or
61 step = sieve.pop(candidate)
62 elif candidate < prime_squared: # prime, or
63 yield candidate
64 continue
65 else: # the next base prime's square
66 # if candidate != prime_squared:
67 # raise ValueError()
68 step = prime * 2
69 prime = next(recurse)
70 prime_squared = prime * prime
71 candidate += step # the next multiple
72 while candidate in sieve: # make sure to not overwrite another sieve entry
73 candidate += step
74 sieve[candidate] = step
75
76
77def prime_factors(num: int) -> Iterator[int]:
78 """Iterates over the prime factors of a number.
79
80 .. note::
81
82 For the purposes of this function, :math:`-1` is included as a factor for negative numbers, and :math:`0` is
83 yielded as a special case. In general, prime factors are strictly positive integers greater than 1.
84
85 It takes :math:`O(m \\cdot \\log(m)^{1.585} \\cdot \\log(\\log(m)))` time to generate the needed primes, where
86 :math:`m = \\sqrt{n}`, so :math:`O(\\sqrt{n} \\cdot \\log(\\sqrt{n})^{1.585} \\cdot \\log(\\log(\\sqrt{n})))`,
87 which simplifies to :math:`O(\\sqrt{n} \\cdot \\log(n)^{1.585} \\cdot \\log(\\log(n)))` operations."""
88 if num < 0:
89 yield -1
90 num = -num
91 if num == 0:
92 yield 0
93 else:
94 root = ceil(sqrt(num))
95 for factor in primes():
96 modulo = num % factor
97 if modulo == 0:
98 while modulo == 0: # double-check to call sqrt once
99 yield factor
100 num //= factor
101 modulo = num % factor
102 root = ceil(sqrt(num))
103 if num <= 1:
104 break
105 if factor > root:
106 yield num
107 break
108
109
110def is_prime(
111 num: int,
112 count: int = 1,
113 distinct: bool = False
114) -> bool:
115 """Detects if a number is prime or not.
116
117 If a count other than 1 is given, it returns True only if the number has exactly count prime factors.
118
119 This function has three cases. If count is :math:`1`, this function runs in
120 :math:`O(\\log(n)^{1.585} \\cdot \\log(\\log(n)))`. If count is :math:`c` and ``distinct=False``, it runs in
121 :math:`O(c \\cdot \\log(n)^{1.585} \\cdot \\log(\\log(n)))`. Otherwise, it runs in
122 :math:`O(\\sqrt{n} \\cdot \\log(n)^{1.585} \\cdot \\log(\\log(n)))` time."""
123 if num < 2:
124 return False
125 factors = iter(prime_factors(num))
126 if count == 1:
127 if num in cache: # always has 2
128 return True
129 if num % 2 == 0:
130 return False
131 return next(factors) == num
132 seen: Collection[Optional[int]]
133 seen_add: Callable[[Optional[int]], None]
134 if distinct:
135 seen = set()
136 seen_add = seen.add
137 else:
138 seen = []
139 seen_add = seen.append
140 while None not in seen and count != len(seen):
141 seen_add(next(factors, None))
142 return None not in seen and next(factors, None) is None
143
144
145def primes_and_negatives(*args: int) -> Iterator[int]:
146 """Iterate over the primes and their negatives using :py:func:`primes`."""
147 for p in primes(*args):
148 yield p
149 yield -p
150
151
152def fast_totient(n: int, factors: Optional[Iterable[int]] = None) -> int:
153 """A faster method to calculate Euler's totient function when n has *distinct* prime factors.
154
155 It runs exactly 1 multiplication and 1 subtraction per prime factor, giving a worst case of
156 :math:`O(\\sqrt{n} \\cdot \\log(n)^{3.17} \\cdot \\log(\\log(n)))`."""
157 return reduce(lambda x, y: x * (y - 1), factors or prime_factors(n), 1)
158
159
160def _reduce_factors(x: Fraction, y: int) -> Fraction:
161 return x * Fraction(y - 1, y)
162
163
164def totient(n: int) -> int:
165 """Calculates Euler's totient function in the general case.
166
167 This function computes the number of integers less than n that are coprime to n. It handles the general case,
168 including repeated prime factors.
169
170 Takes :math:`O(\\log(n))` fraction multiplications, each of which is dominated by two GCDs, which run at
171 :math:`O(\\log(\\min(a, b))^2)`. Given that the max factor is :math:`\\sqrt{n}`, we can simplify this to a worst
172 case of :math:`O(\\log(n) \\cdot \\log(\\sqrt{n}))^2 = O(\\log(n) \\cdot \\tfrac{1}{2} \\log(n)^2) = O(\\log(n)^3)`.
173
174 Computing the prime factors themselves takes :math:`O(\\sqrt{n} \\cdot \\log(n)^{1.585} \\cdot \\log(\\log(n)))`
175 when the global prime cache is not initialized, but on all future runs will take :math:`O(\\log(n))` time.
176
177 This combines to give us :math:`O(\\sqrt{n} \\cdot \\log(n)^{4.585} \\cdot \\log(\\log(n)))` time when the cache is
178 stale, and :math:`O(\\log(n)^4)` time on future runs."""
179 total_factors = tuple(prime_factors(n))
180 unique_factors = set(total_factors)
181 if len(total_factors) == len(unique_factors):
182 return fast_totient(n, unique_factors)
183
184 fractional = reduce(_reduce_factors, unique_factors, Fraction(1, 1))
185 return int(n * fractional)