primes.js

View source code here on GitHub!

primes.primes(stop=null)

Iterates over the prime numbers up to an (optional) limit, with caching.

This iterator leverages the primes.modifiedEratosthenes() iterator, but adds additional features. The biggest is a stop argument, which will prevent it from yielding any numbers larger than that. The next is caching of any yielded prime numbers.

Arguments:

  • stop (number|null)

primes.modifiedEratosthenes()

Iterates over prime numbers using the Sieve of Eratosthenes.

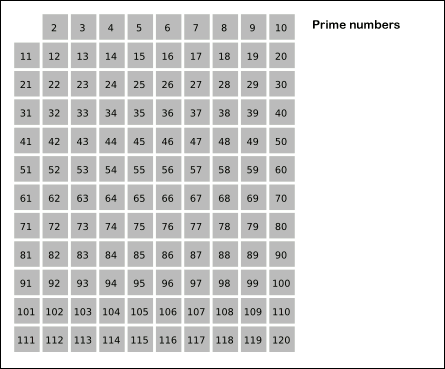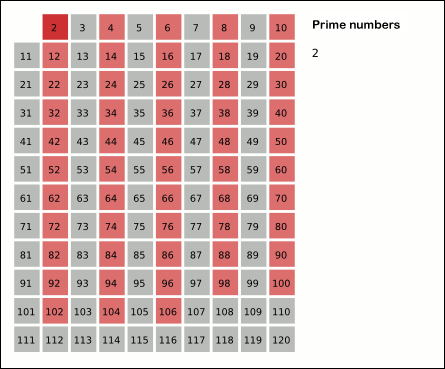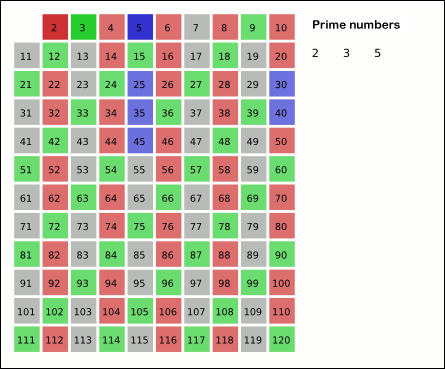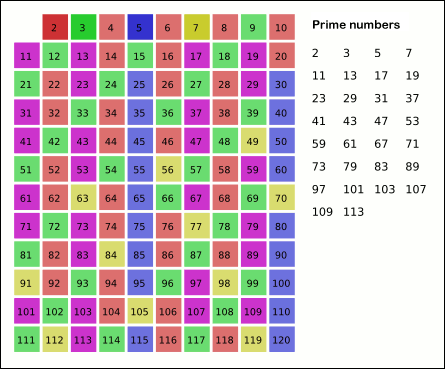
This function implements the Sieve of Eratosthenes. In general, it will iterate over all of the prime numbers. Below is a gif (courtesy of Wikipedia) that demonstrates the principle of the sieve.

Any animated example of the Sieve of Eratosthenes
primes.primeFactors(num)

Iterates over the prime factors of a number.

Arguments:

  • num (number)

primes.primesAndNegatives(stop=null)

Iterates over the prime numbers (and their negatives) up to an (optional) limit, with caching.

This iterator leverages the primes.primes() iterator.

Arguments:

  • stop (number|null)

primes.isComposite(n)

Tests if a number is composite

Arguments:

  • n (number)

Returns:

number -- 0 if prime, or the first prime factor if not

primes.isPrime(n)

Tests if a number is prime

Arguments:

  • n (number)

Returns:

boolean --

  1const cache = [2, 3, 5, 7];
  2let lastCached = 7;
  3
  4/**
  5 * Iterates over the prime numbers up to an (optional) limit, with caching.
  6 *
  7 * This iterator leverages the :js:func:`primes.modifiedEratosthenes` iterator, but adds
  8 * additional features. The biggest is a ``stop`` argument, which will prevent it
  9 * from yielding any numbers larger than that. The next is caching of any yielded
 10 * prime numbers.
 11 * @param {number | null} stop
 12 * @yield {number}
 13 */
 14function* primes(stop = null) {
 15    if (stop === null) {
 16        for (const p of cache) {
 17            yield p;
 18        }
 19    } else {
 20        for (const p of cache) {
 21            if (p < stop) {
 22                yield p;
 23            } else {
 24                break;
 25            }
 26        }
 27    }
 28    if (stop !== null && lastCached > stop) {
 29        return;
 30    }
 31    for (const p of modifiedEratosthenes()) {
 32        if (p <= lastCached) {
 33            continue;
 34        }
 35        if (stop !== null && p > stop) {
 36            break;
 37        }
 38        cache.push(p);
 39        lastCached = p;
 40        yield p;
 41    }
 42}
 43exports.primes = primes;
 44
 45
 46/**
 47 * Iterates over prime numbers using the Sieve of Eratosthenes.
 48 *
 49 * This function implements the `Sieve of Eratosthenes <https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes>`_. In
 50 * general, it will iterate over all of the prime numbers. Below is a gif (courtesy of Wikipedia) that demonstrates
 51 * the principle of the sieve.
 52 *
 53 * .. image:: https://upload.wikimedia.org/wikipedia/commons/9/94/Animation_Sieve_of_Eratosth.gif
 54 *      :alt: Any animated example of the Sieve of Eratosthenes
 55 * @yield {number}
 56 */
 57function* modifiedEratosthenes() {
 58    yield 2;
 59    yield 3;
 60    yield 5;
 61    yield 7;
 62    const sieve = new Map();
 63    const recurse = primes();
 64    recurse.next();
 65    let prime = recurse.next().value;
 66    if (prime !== 3) {
 67        throw new Error();
 68    }
 69    let primeSquared = prime * prime;
 70    let step = 2;
 71    for (let candidate = 9; ; candidate += 2) {
 72        if (sieve.has(candidate)) { // if c is a multiple of some base prime, or
 73            step = sieve.get(candidate);
 74            sieve.delete(candidate);
 75        } else if (candidate < primeSquared) { // prime, or
 76            yield candidate;
 77            continue;
 78        } else { // the next base prime's square
 79            // if candidate != primeSquared:
 80            //     raise ValueError()
 81            step = prime * 2;
 82            prime = recurse.next().value;
 83            primeSquared = prime * prime;
 84        }
 85        let tc = candidate;
 86        do {
 87            tc += step; // the next multiple
 88        } while (sieve.has(tc)); // make sure to not overwrite another sieve entry
 89        sieve.set(tc, step);
 90    }
 91}
 92exports.modifiedEratosthenes = modifiedEratosthenes;
 93
 94
 95/**
 96 * Iterates over the prime factors of a number.
 97 *
 98 * @param {number} num
 99 * @yield {number}
100 */
101function* primeFactors(num) {
102    if (num < 0) {
103        yield -1;
104        num = -num;
105    }
106    if (num === 0) {
107        yield 0;
108    } else {
109        let root = Math.ceil(Math.sqrt(num));
110        for (const factor of primes()) {
111            let modulo = num % factor;
112            if (modulo == 0) {
113                while (modulo == 0) { // double-check to call sqrt once
114                    yield factor;
115                    num /= factor;
116                    modulo = num % factor;
117                }
118                root = Math.ceil(Math.sqrt(num));
119            }
120            if (num <= 1) {
121                break;
122            }
123            if (factor > root) {
124                yield num;
125                break;
126            }
127        }
128    }
129}
130exports.primeFactors = primeFactors;
131
132/**
133 * Iterates over the prime numbers (and their negatives) up to an (optional) limit, with caching.
134 *
135 * This iterator leverages the :js:func:`primes.primes` iterator.
136 * @param {number | null} stop
137 * @yield {number}
138 */
139function* primesAndNegatives(stop = null) {
140    for (const p of primes(stop)) {
141        yield p;
142        yield -p;
143    }
144}
145exports.primesAndNegatives = primesAndNegatives;
146
147/**
148 * Tests if a number is composite
149 * @param {number} n
150 * @return {number} 0 if prime, or the first prime factor if not
151 */
152function isComposite(n) {
153    const factors = primeFactors(n);
154    const first = factors.next().value;
155    if (factors.next().done) {
156        return 0;
157    }
158    return first;
159}
160exports.isComposite = isComposite;
161
162/**
163 * Tests if a number is prime
164 * @param {number} n
165 * @return {boolean}
166 */
167function isPrime(n) {
168    if (n < 2) {
169        return false;
170    }
171    return !isComposite(n);
172}
173exports.isPrime = isPrime;

Tags: prime-number, divisibility, factorization, js-iterator