prime.cs
View source code here on GitHub!
Includes
- class Prime
- static IEnumerable<T> Primes<T> (T? stop = null)
This function implements the Sieve of Eratosthenes. In general, it will iterate over all of the prime numbers. You can also provide an optional
stopargument, which will force it to not yield any numbers above that limit. Below is a gif (courtesy of Wikipedia) that demonstrates the principle of the sieve.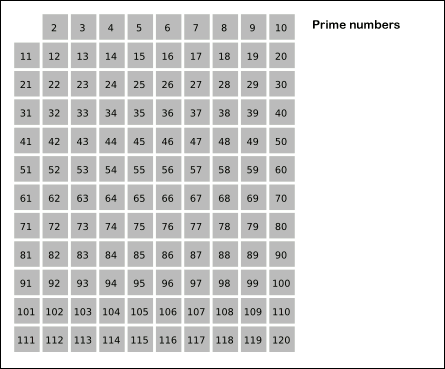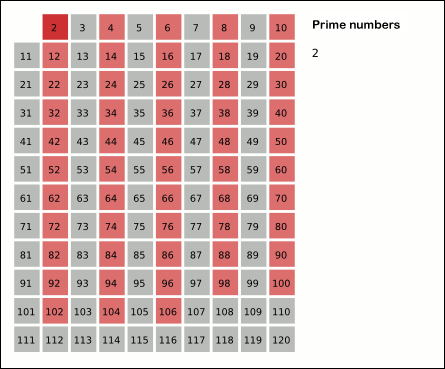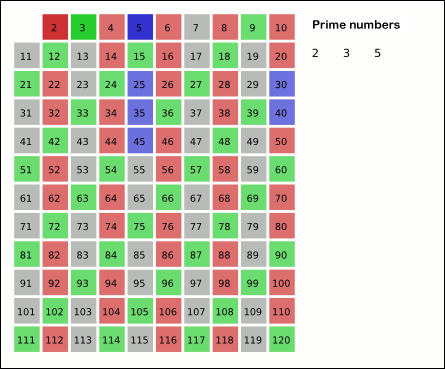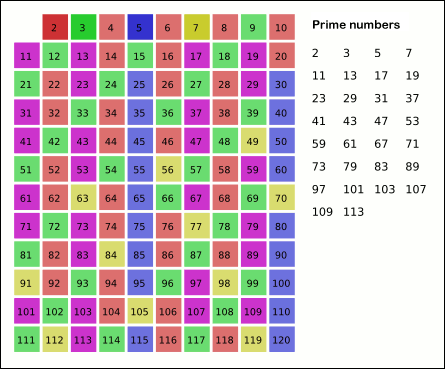
- static IEnumerable<T> PrimeFactors<T> (T n)
This function will iterate over all the prime factors of a number, as well as
-1and0if relevant.
1using System;
2using System.Collections.Generic;
3
4namespace Euler
5{
6 public static class Prime
7 {
8 private static readonly Dictionary<Type, (dynamic LastCached, List<dynamic> Cache)> Caches = new();
9
10 public static IEnumerable<T> Primes<T>(T? stop = null) where T : struct
11 {
12 foreach (dynamic p in _Primes(stop))
13 yield return (T)p;
14 }
15
16 private static IEnumerable<dynamic> _Primes(dynamic? stop = null)
17 {
18 Type type = stop != null ? stop.GetType() : typeof(long);
19 if (!Caches.TryGetValue(type, out var cacheData))
20 {
21 cacheData = (LastCached: (dynamic)0, Cache: new List<dynamic>());
22 Caches[type] = cacheData;
23 }
24 (dynamic lastCached, List<dynamic> cache) = cacheData;
25
26 // Yield cached values
27 if (stop == null)
28 foreach (dynamic p in cache)
29 yield return p;
30 else
31 foreach (dynamic p in cache)
32 if (p < stop)
33 yield return p;
34 else
35 break;
36
37 // Generate new primes
38 if (stop != null && lastCached > stop)
39 yield break;
40
41 foreach (dynamic p in ModifiedEratosthenes())
42 {
43 if (p <= lastCached)
44 continue;
45 if (stop != null && p > stop)
46 break;
47
48 cache.Add(p);
49 lastCached = p;
50 Caches[type] = (lastCached, cache);
51 yield return p;
52 }
53 }
54
55 private static IEnumerable<dynamic> ModifiedEratosthenes()
56 {
57 yield return 2;
58 yield return 3;
59 yield return 5;
60 yield return 7;
61 var sieve = new Dictionary<dynamic, dynamic>();
62 var recurse = ModifiedEratosthenes().GetEnumerator();
63 recurse.MoveNext();
64 recurse.MoveNext();
65 dynamic prime = recurse.Current;
66 if (prime != 3)
67 throw new Exception();
68 dynamic primeSquared = prime * prime;
69 dynamic step = 2;
70 for (dynamic candidate = 9; ; candidate += 2)
71 {
72 if (sieve.ContainsKey(candidate))
73 {
74 step = sieve[candidate];
75 sieve.Remove(candidate);
76 }
77 else if (candidate < primeSquared)
78 {
79 yield return candidate;
80 continue;
81 }
82 else
83 {
84 step = prime * 2;
85 recurse.MoveNext();
86 prime = recurse.Current;
87 primeSquared = prime * prime;
88 }
89 dynamic tc = candidate;
90 do
91 {
92 tc += step;
93 } while (sieve.ContainsKey(tc));
94 sieve.Add(tc, step);
95 }
96 }
97
98 public static IEnumerable<T> PrimeFactors<T>(T n) where T : struct
99 {
100 foreach (dynamic f in _PrimeFactors(n))
101 yield return (T)f;
102 }
103
104 private static IEnumerable<dynamic> _PrimeFactors(dynamic n)
105 {
106 if (n < 0)
107 {
108 yield return -1;
109 n = -n;
110 }
111 if (n == 0)
112 yield return 0;
113 else
114 {
115 dynamic root = (dynamic)Math.Ceiling(Math.Sqrt((double)n));
116 foreach (dynamic factor in _Primes())
117 {
118 dynamic modulo = n % factor;
119 if (modulo == 0)
120 {
121 do
122 {
123 yield return factor;
124 n /= factor;
125 modulo = n % factor;
126 } while (modulo == 0);
127 root = (dynamic)Math.Ceiling(Math.Sqrt((double)n));
128 }
129 if (n <= 1)
130 break;
131 if (factor > root)
132 {
133 yield return n;
134 break;
135 }
136 }
137 }
138 }
139
140 public static dynamic IsComposite(dynamic n)
141 {
142 var factors = PrimeFactors(n).GetEnumerator();
143 factors.MoveNext();
144 dynamic first = factors.Current;
145 if (first == n)
146 return 0;
147 return first;
148 }
149
150 public static bool IsPrime(dynamic n)
151 {
152 if (n < 2)
153 return false;
154 return IsComposite(n) == 0;
155 }
156 }
157}